Тест: 15 вопросов
1.
Площадь практически любой трапеции (не имеющей прямые углы) является возможным найти, разделив на некоторые фигуры:
два треугольника и прямоугольник;
один треугольник и квадрат;
один прямоугольник и треугольник;
два квадрата.
2.
Площадь каждой трапеции - это...
поверхность, составленная из квадратов;
поверхность, обнесённая треугольником;
часть поверхности, ограниченная двумя параллельными и двумя не параллельными прямыми;
участок поверхности, ограниченный парами взаимно параллельных прямых.
3.
Площадь прямоугольной трапеции можно вычислить, если поделить поверхность фигуры на несколько частей. Они будут являться:
ромбом и треугольником;
треугольниками;
квадратами;
прямоугольником и треугольником.
4.
Для вычисления площади трапеции, нужно:
умножить половину суммы оснований на высоту трапеции;
разделить пол суммы оснований на высоту;
умножить одно из оснований на высоту;
разделить меньшее основание на высоту трапеции.
5.
Прямоугольная трапеция имеет меньшее основание длиной 6 см. Меньшая боковая сторона тоже равна 6 см, а тупой угол имеет значение 135°. Требуется указать верную площадь.
108;
36;
9;
54.
6.
Есть трапеция с прямым углом. Её высота делит большее основание на отрезки 3,3 см и 1,7 см. Тупой угол равен 135°. Требуется выяснить длину высоты и меньшего основания данной трапеции?
высота 3,3, а основание 1,7;
основание 3,3, а высота 1,7;
высота 1,7, а основание 5;
основание 3, 3, а высота 5.
7.
Большее основание равнобедренной трапеции разделено высотой на два отрезка длиной 4 см и 2 см. Самый большой угол равен 135°. Чему будет равняться площадь фигуры?
9;
12;
8;
24.
8.
Основания трапеции равны 10 см и 6 см. Высота равна 4 см. Необходимо посчитать площадь данной трапеции.
16;
18;
24;
32.
9.
Высота трапеции равна половине длины меньшего основания. Основания равны 16 см и 12 см. Требуется указать верное значение площади трапеции.
28;
56;
20;
84.
10.
Дан рисунок. Указать верное значение средней линии трапеции.
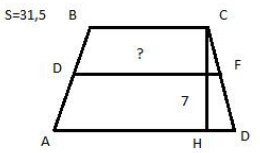
4,5;
9;
7;
8.
11.
Дана средняя линия трапеции, длиной 7 см. Высота равна 3 см. Площадь этой фигуры имеет следующее значение:
9,5;
21;
49;
63.
12.
Каким образом можно найти площадь трапеции?
умножив любое из оснований на высоту;
умножив боковую сторону на высоту;
поделив среднюю линию трапеции на высоту;
умножив среднюю линию трапеции на высоту.
13.
Требуется определить по рисунку, какая прямая будет являться средней линией трапеции:
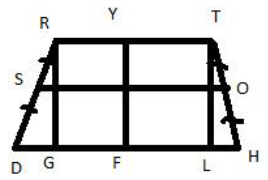
SO;
RG;
TL;
YF.
14.
В прямоугольной трапеции нужно найти острый угол, если даны длины оснований 5 и 13, а площадь 81.
45°;
35°;
55°;
65°.
15.
Известна площадь трапеции. Она равна 64. Имеется, также, средняя линия, равная 8. Тогда высота данной трапеции будет:
8;
64;
16;
24.
Для максимально эффективной подготовки к предстоящему зачету или экзамену по математике используйте бесплатное тестирование на нашем сайте. В ходе работы над вопросами теста вы не только проверите свой уровень знаний, но и закрепите изученный ранее материал и обнаружите пробелы, над которыми стоит поработать. Проходите тестирование несколько раз, повторяйте темы и термины, систематизированные специалистами специально для вас.
Заказать решение тестов по математике у экспертов биржи Студворк!
Комментарии