На рисунке изображены две похожие фигуры. В каком из вариантов они будут подобными?
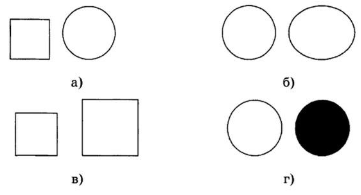
а;
г;
б;
в.
Сколько подобных треугольников изображено на этом рисунке?
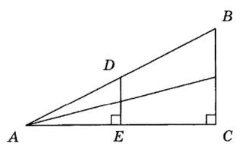
2;
4;
1;
3.
В треугольнике ABC угол А = 80°, угол B=15°, сторона АВ = 3. В треугольнике A1B1C1 угол В1 = 80°, угол С1=85°, сторона A1B1 равна 9. Являются ли треугольники ABC и A1B1C1 подобными? Почему?
не являются, так как не справедлив ни один из признаков подобия;
являются, так как 2 угла 1-го треугольника соответственно равны 2-м углам другого треугольника;
являются, так как 2 стороны одного треугольника пропорциональны 2-м сторонам другого треугольника, а углы между этими сторонами равны;
являются, так как 3 стороны одного треугольника пропорциональны 3-м сторонам другого треугольника.
Подобны ли равнобедренные треугольники, приведённые на рисунке?
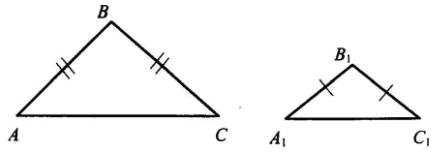
Треугольники не являются подобными;
треугольники являются подобными по 2-м пропорциональным сторонам и равным углам между ними;
треугольники являются подобными по 2-м равным углам;
в условии не хватает данных для решения задачи.
Дана задача: «Треугольники MKE и M1K1E1 подобны. MK = 4, KE = 5, EM=3. Коэффициент подобия равен 2 (треугольник M1K1E1 больше). Найдите отношение периметров этих треугольников». Ниже приведено ее решение. В одном из этапов допущена ошибка. В ответе укажите номер этого этапа.
Решение:
1) Периметр треугольника MKE = MK + KE + EM = 4 + 5 + 3 = 12.
2) Так как треугольники подобны, стороны треугольника M1K1E1 можно найти по формулам:
M1K1 = MK/2 =4/2=2;
K1E1 = KE/2=5/2=2,5;
E1M1 = EM/2=3/2=1,5.
3) Периметр треугольника M1K1E1 = M1K1 + K1E1 + E1M1 = 2 + 2,5 + 1,5 = 6.
4) Отношение периметров треугольников MKE и M1K1E1 равно 12:6=2.
Выберите правильный ответ:
1;
2;
3;
4.
На рисунках изображены два треугольника. Являются ли они подобными? Если да, чему равен коэффициент подобия? Учитывайте размер клеток на рисунках - 1х1.
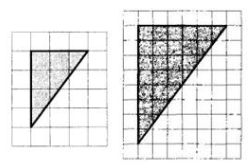
треугольники подобными не будут;
треугольники считаются подобными, коэффициент подобия 1,5;
треугольники подобные, с коэффициентом подобия 2;
треугольники подобные, их коэффициент подобия 4.
Треугольники ABC и LRE подобны: 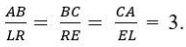 MN = средняя линия в треугольнике ABC. Найдите коэффициент подобия треугольников LRE и MBN.
MN = средняя линия в треугольнике ABC. Найдите коэффициент подобия треугольников LRE и MBN.
1,5;
2;
4;
эти треугольники не будут подобными.
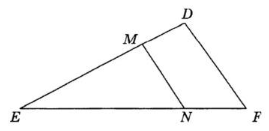
В треугольнике EDF был проведён отрезок MN параллельно отрезку DF. Чему будет равен коэффициент подобия получившихся треугольников, если известно, что длина EN = 4 см, а NF= 1 см.
4;
1/4;
5;
4/5 или 5/4.
Для максимально эффективной подготовки к предстоящему зачету или экзамену по математике используйте бесплатное тестирование на нашем сайте. В ходе работы над вопросами теста вы не только проверите свой уровень знаний, но и закрепите изученный ранее материал и обнаружите пробелы, над которыми стоит поработать. Проходите тестирование несколько раз, повторяйте темы и термины, систематизированные специалистами специально для вас.
Заказать решение тестов по математике у экспертов биржи Студворк!



Комментарии