Какой из углов на представленном рисунке будет центральным, если Q - центр окружности?
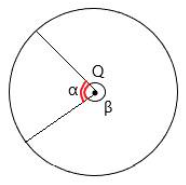
угол α
угол β
угол α и угол β
ни один из углов
Градусная мера центрального угла равна градусной мере … Вставьте пропущенное утверждение:
градусной мере дуги, на которую он опирается
градусной мере прямого угла
градусной мере вписанного угла, опирающегося на ту же дугу
градусной мере дуги, на которую опирается диаметр окружности
На рисунке представлена окружность с центром в точке Q. Известно, что угол RKN=130°. Необходимо найти величину угла RQN.
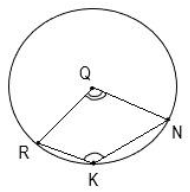
80°
160°
100°
50°
Выберите формулу для нахождения длины дуги, на которую опирается центральный угол, если центральный угол равен α, а радиус равен r:
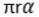
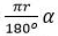
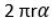
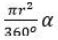
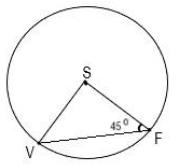
Треугольник VSF вписан в окружность с центром S. Угол SFV=45°, необходимо найти центральный угол VSF.
75°
100°
120°
90°
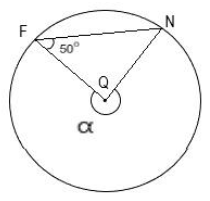
Найдите угол α, если известно, что угол QFN=50°, а точка Q является центром окружности.
260°
280°
320°
300°
Отрезок FB является диаметром окружности. Центральный угол FQH=32°, угол BQN=47°. Найдите угол β.
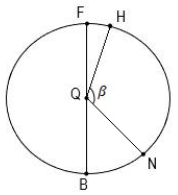
111°
101°
107°
117°
Для максимально эффективной подготовки к предстоящему зачету или экзамену по математике используйте бесплатное тестирование на нашем сайте. В ходе работы над вопросами теста вы не только проверите свой уровень знаний, но и закрепите изученный ранее материал и обнаружите пробелы, над которыми стоит поработать. Проходите тестирование несколько раз, повторяйте темы и термины, систематизированные специалистами специально для вас.
Заказать решение тестов по математике у экспертов биржи Студворк!
Комментарии