Тест: 15 вопросов
1.
Преобразуйте выражение (x – 1)(x – 2) в многочлен стандартного вида:
2x – 3;
x2 – 3x + 2;
x2 – 2;
x2 + 2x + 2.
2.
Представьте произведение 2y(y – 3)(y + 1) – 2y(y2 + 3) в виде многочлена:
- 2y3 – 2y2 – 3;
2y3 – 6y2 – 6y – 3;
-4y2 – 12y;
4y2 – 6y – 3.
3.
После выполнения тождественных преобразований выражение –m(2m + 1)(m - 1) примет вид:
m3 + 2m2 – m;
2m3 + m2;
-m2 + m;
-2m3 + m2 + m.
4.
В каком случае произведение преобразовано правильно:
(x + 3)(x – 2) = x2 + x + 6;
(2 – x)(1 – x) = -x2 – 3x + 2;
(x – 3)(1 + x) = x2 + 2x – 3;
(x + 1)(2 – x) = -x2 + x + 2.
5.
Выберите вариант, где при умножении многочленов была сделана ошибка:
(4x + 7)(2 – 3x) = 12x2 – 13x + 14;
(2 – 1,5x)(4x + 6) = - 6x2 – x + 12;
(2x + 3)(3 – x) = -2x2 + 3x + 9;
(3 – 5x)(3 – 3x) = 15x2 – 24x + 9.
6.
Корнем уравнения (x + 2)(3 – x) + x2 = 2(6 – x) будет:
x = -1;
x = -2;
x = 1;
x = 2.
7.
Степень многочлена, получившегося после преобразования выражения x(x + 1)(x – 2) будет равна:
3;
2;
1;
0.
8.
При любом m значение выражения (-m + 7)(-m – 2) – m(m – 5) равно:
-10 m – 14;
1;
0;
-14.
9.
Площадь прямоугольника, изображенного на рисунке, равна:
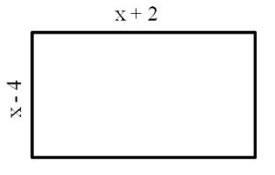
x2 – 2x – 8;
x2 – 8;
x2 – 6;
2x – 2.
10.
При любом значении y значение выражения (2y + 3)(y – 5) – 2y(y – 2) делится на число:
4;
3;
6;
2.
11.
Значение выражения 2y(2 – y)(y + 3) при y = -2 равно:
-48;
12;
16;
-16.
12.
Найдите тождественно равные выражения:
(a + 1)(a – 2) и (a + 3)(a – 2) + 6;
(a + 8)(2a – 2) и (a + 4)(2a – 4) + 10a;
(2a – 3)(3a + 2) и (3a – 2)(2a + 3);
(3a + 5)(2a + 7) и (3a + 7)(2a + 5).
13.
Определите, какие выражения не являются тождественно равными:
(x + 3)(2x – 4) и 2(x2 + x – 6);
(x + 1)(x – 1) и x2 – 1;
(2x – 5)(x + 3) и 2x2 –x – 15;
(3x + 1)(x – 7) и 3x2 – 20x – 7.
14.
Даны три последовательно натуральных числа, такие, что произведение первого и второго на 34 меньше произведения второго и третьего. С помощью какого уравнения можно решить эту задачу?
2x + 34 = x(x + 2);
2x – 3x = 34;
x(x + 1)(x + 2) = 34;
x(x + 1) + 34 = (x + 1)(x + 2).
15.
Значение выражения (b + 21)(b – 3) – (b + 27)(b – 4) при всех натуральных значениях b кратно числу:
7;
5;
4;
3.
Для максимально эффективной подготовки к предстоящему зачету или экзамену по математике используйте бесплатное тестирование на нашем сайте. В ходе работы над вопросами теста вы не только проверите свой уровень знаний, но и закрепите изученный ранее материал и обнаружите пробелы, над которыми стоит поработать. Проходите тестирование несколько раз, повторяйте темы и термины, систематизированные специалистами специально для вас.
Заказать решение тестов по математике у экспертов биржи Студворк!
Комментарии