Тест по квадратичной функции с готовыми ответами для студентов

Тест: 15 вопросов

Квадратичная функция представляет собой:

уравнение вида bx2+ax+c, где a и b – коэффициенты, а с – свободный член, причем a≠0;

уравнение вида ax2+bx+c, где a и b – коэффициенты, а с – свободный член, причем a≠0;

уравнение вида ax2+bx+c, где a и b – коэффициенты, а с – свободный член, причем c≠0;

уравнение вида ax2+bx+c, где a и b – коэффициенты, а с – свободный член, причем b≠0.

2. Частным случаем квадратичной функции является:

x2/a2 -y2/b2 =1 – гипербола;

y=x3 – кубическая парабола;

y=x2 – квадратичная парабола;

y=√x – степенная функция.

3. При каком условии квадратичная функция при любых значениях коэффициентов будет иметь такую же форму, как и квадратичная парабола y=x2:

при старшем коэффициенте неравном единице (a≠1);

при коэффициентах неравных нулю (a≠0,b≠0 и c≠0);

при отсутствии свободного члена (c=1);

при старшем коэффициенте равном единице (a=1).

Если старший коэффициент в квадратичной функции будет отрицателен (a<0), то ветви полученной параболы будут направлены:

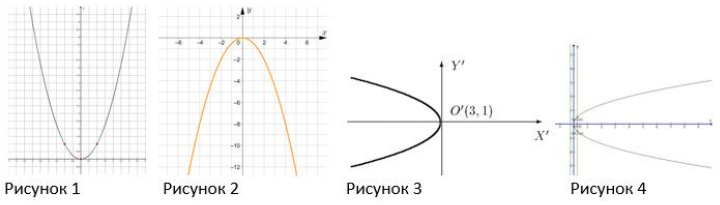
вниз, как на рисунке 2;

вверх, как на рисунке 1;

влево, как на рисунке 3;

вправо, как на рисунке 4.

5. Если старший коэффициент в квадратичной функции будет положителен (a>0), то ветви полученной параболы будут направлены:

вниз, как на рисунке 2;

вверх, как на рисунке 1;

влево, как на рисунке 3;

вправо, как на рисунке 4.

6. Нуль функции f(x) – это

точка функции, проходящая через ноль координатной плоскости;

точка пересечения графика функции y=f(x) с осью ОХ;

точка пересечения графика функции y=f(x) с осью ОY;

точка, не входящая в диапазон решения.

7. Укажите верную формулу нахождения корней квадратного уравнения ax2+bx+c=0:

D=b2-4ac. x1,2=(-b±√D)/2a;

D=k2-ac, где k – это двойное значение b. x1,2=(-k±√D)/a;

D=k2-ab, где k – это двойное значение b. x1,2=(-k±√D)/a;

D=b2-4a. x1,2=(-b±√D)/a.

8. Соотнеси рисунок с полученным дискриминантом при решении квадратного уравнения 2x2+4x+8=0:

Дискриминант отрицательный, поэтому рисунок 5;

Дискриминант отрицательный, поэтому рисунок 6;

Дискриминант отрицательный, поэтому рисунок 7;

не имеет графического решения.

9. Соотнеси рисунок с полученным дискриминантом при решении квадратного уравнения x2-2x+1=0:

Дискриминант равен нулю, поэтому рисунок 5;

Дискриминант равен нулю, поэтому рисунок 6;

Дискриминант равен нулю, поэтому рисунок 7;

не имеет графического решения.

10.

Соотнеси рисунок с полученным дискриминантом при решении квадратного уравнения x2-x-5=0:

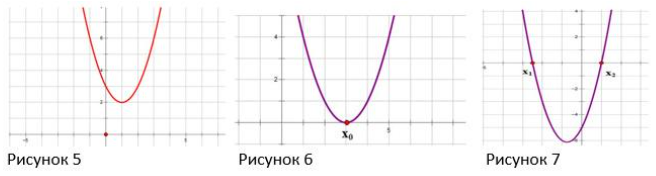
Дискриминант положителен, поэтому рисунок 5;

Дискриминант положителен, поэтому рисунок 6;

Дискриминант положителен, поэтому рисунок 7;

не имеет графического решения.

11. Координаты вершины параболы можно найти по формулам:

x0=b/2a; y0=D/4a;

x0=-b/2a; y0=-D/4a;

x0=-b/4a; y0=-D/2a;

x0=b/4a; y0=D/2a.

12. Осью симметрии параболы называют:

прямую, проходящую через ноль координатной плоскости параллельно оси OX;

прямую, проходящую через ноль координатной плоскости параллельно оси OY;

прямую, проходящую через вершину параболы параллельно оси OY;

прямую, проходящую через вершину параболы параллельно оси OX.

13. Как найти точку пересечения параболы с осью ординат OY:

необходимо в квадратное уравнение y=ax2+bx+c подставить вместо неизвестного х ноль, тогда ордината будет равна c, а абсцисса нулю;

необходимо в квадратное уравнение y=ax2+bx+c подставить вместо неизвестного х ноль, тогда ордината и абсцисса будут равны c;

необходимо квадратное уравнение y=ax2+bx+c приравнять к нулю, тогда первый корень — это ордината, а значение второго абсцисса;

необходимо в квадратное уравнение y=ax2+bx+c подставить вместо неизвестного х ноль, тогда ордината будет равна нулю, а абсцисса с.

14. Какое свойство квадратичной функции y=ax2 неверно для старшего коэффициента больше нуля a>0:

область определения от -∞ до +∞;

если x=0, то y=0, то есть график функции проходит через начало координат;

если x≠0, то y

при x=0 функция принимает наименьшее значение, равное нулю, а наибольшего значения функции на бесконечном промежутке не существует.

15.

Какое свойство квадратичной функции y=ax2 верно для старшего коэффициента меньше нуля a<0:

область определения от 0 до +∞;

если x=0, то y≠0, то есть график функции не проходит через начало координат;

если x≠0, то y<0, то есть график функции расположен в нижней полуплоскости;

Для максимально эффективной подготовки к предстоящему зачету или экзамену по математике используйте бесплатное тестирование на нашем сайте. В ходе работы над вопросами теста вы не только проверите свой уровень знаний, но и закрепите изученный ранее материал и обнаружите пробелы, над которыми стоит поработать. Проходите тестирование несколько раз, повторяйте темы и термины, систематизированные специалистами специально для вас.

Заказать решение тестов по математике у экспертов биржи Студворк!

Квадратичная функция

Комментарии
0

Предыдущая статья

Следующая статья

Интересные статьи за сегодня

Квадратичная функция

Комментарии 0

Предыдущая статья

Следующая статья

Интересные статьи за сегодня

Комментарии
0